How Levenshtein works...
The Levenshtein algorithm (also called Edit-Distance) calculates the least number
of edit operations that are necessary to modify one string to obtain another string.
The most common way of calculating this is by the dynamic programming
approach. A matrix is initialized measuring in the (m,n)-cell the Levenshtein
distance between the m-character prefix of one with the n-prefix of the other
word. The matrix can be filled from the upper left to the lower right corner. Each
jump horizontally or vertically corresponds to an insert or a delete, respectively.
The cost is normally set to 1 for each of the operations. The diagonal jump can
cost either one, if the two characters in the row and column do not match or 0, if
they do. Each cell always minimizes the cost locally. This way the number in the
lower right corner is the Levenshtein distance between both words. Here is an
example that features the comparison of "meilenstein" and "levenshtein":
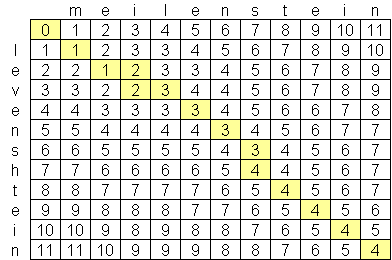
There are two possible paths through the matrix that actually produce the least cost solution. Namely

"=" Match; "o" Substitution; "+" Insertion; "-" Deletion
Though there are sophisticated improvements on the complexity, there is no
alternative to calculating the matrix to at least a large extent. To the author's knowledge
the only company to implement the fastest Levensthein Algorithm
is Exorbyte.
|
|
|